Time to heat shaft to a given temperature.xls
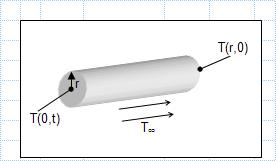
Description
KNOWN: Diameter and radial temperature of AISI 1010 carbon steel shaft Convection coefficient and temperature of furnace gases.
FIND: Time required for shaft centerline to reach a prescribed temperature.
ASSUMPTIONS: 1) One-dimensional, radial conduction.
2) Constant properties.
Calculation Reference
Fundamentals of Heat and Mass Transfer - Frank P. Incropera
To determine the time required for the centerline of an AISI 1010 carbon steel shaft to reach a prescribed temperature, considering the diameter, radial temperature, convection coefficient, and temperature of the furnace gases, you can follow these steps:
-
Calculate the thermal diffusivity: The thermal diffusivity (α) of the AISI 1010 carbon steel can be calculated using the formula:
α = (Thermal Conductivity) / (Density * Specific Heat Capacity)
Where the thermal conductivity, density, and specific heat capacity are properties of AISI 1010 carbon steel.
-
Calculate the Biot number: The Biot number (Bi) characterizes the ratio of internal thermal resistance to external thermal resistance and can be calculated using the formula:
Bi = (Convection Coefficient) * (Shaft Diameter) / (2 * α)
Where the convection coefficient is the coefficient of heat transfer between the shaft and the furnace gases.
-
Determine the temperature difference: The temperature difference between the furnace gases and the centerline of the shaft can be calculated as:
ΔT = (Prescribed Temperature) - (Radial Temperature)
-
Calculate the dimensionless time: The dimensionless time (τ) represents the time required for the centerline of the shaft to reach the prescribed temperature and can be obtained by solving the dimensionless form of the transient heat conduction equation for a cylinder:
τ = (Biot Number)^2 * (Dimensionless Time) / 4
The dimensionless time can be found from tables or numerical solutions for transient heat conduction in cylinders.
-
Determine the actual time: The actual time required for the centerline of the shaft to reach the prescribed temperature can be calculated by multiplying the dimensionless time by the characteristic time scale of the system:
Actual Time = (τ * Shaft Diameter^2) / (4 * α)
By following these steps, you can determine the time required for the centerline of the AISI 1010 carbon steel shaft to reach a prescribed temperature, considering the diameter, radial temperature, convection coefficient, and temperature of the furnace gases. The assumptions of one-dimensional, radial conduction and constant properties allow for simplified analysis.
Calculation Preview
Full download access to any calculation is available to users with a paid or awarded subscription (XLC Pro).
Subscriptions are free to contributors to the site, alternatively they can be purchased.
Click here for information on subscriptions.
