Mass Moments of Inertia

Purpose of calculation:
Moments of Inertia

Calculation Reference
http://hyperphysics.phy-astr.gsu.edu/hbase/mi.html

Calculation Validation
Reproduction of a sample calculation from a published calculation reference.

Calculation Reference

Mass Moments of Inertia

Dynamics

Rotatry Dynamics

The moment of inertia, also known as the mass moment of inertia or the second moment of area, is a measure of an object's resistance to rotational motion about a specific axis. In other words, it quantifies how difficult it is to change an object's rotational state. The moment of inertia depends on the object's mass, its shape, and the distribution of the mass relative to the axis of rotation.

For a point mass, the moment of inertia (I) is calculated as follows:

I = m * r^2

Where: I = moment of inertia m = mass of the point mass r = distance of the point mass from the axis of rotation

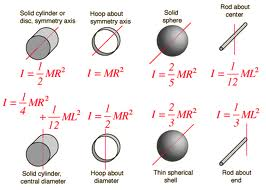
For extended objects with more complex shapes, the moment of inertia is typically calculated by integrating the point mass moment of inertia over the entire object. The moment of inertia of some common shapes is listed below:

1. Solid cylinder or disk about its central axis: I = (1/2) * m * R^2

2. Hollow cylinder about its central axis: I = (1/2) * m * (R1^2 + R2^2)

3. Solid sphere about its diameter: I = (2/5) * m * R^2

4. Rectangular plate about an axis perpendicular to the plane and passing through the center of mass: I = (1/12) * m * (L^2 + W^2)

Where: I = moment of inertia m = mass of the object R = radius of the object R1, R2 = inner and outer radii of the hollow cylinder L, W = length and width of the rectangular plate

The moment of inertia plays a significant role in the study of mechanics, particularly in the analysis of rotational motion, torsion, and structural stability.