Design of chord length

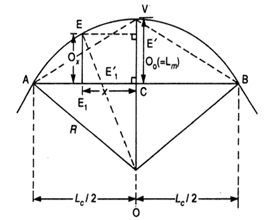
Setting out of chord length for circular curve

Calculation Reference

Circular Geometry

Geometry

Chord Length

Setting out a circular curve using chord lengths is a technique often used in surveying, road, and railway design. The chord length is the straight-line distance between two points on the circular curve. The following steps describe how to calculate the chord length for a given circular curve.

1. Determine the curve parameters:

• R: Radius of the circular curve
• Δ (delta): Central angle subtended by the curve (in degrees)

2. Choose the number of chords (n) to divide the curve into equal parts. The more chords you use, the more accurate the approximation will be.

3. Calculate the chord angle (α) in degrees: α = Δ / n

4. Convert the chord angle (α) to radians: α_rad = α * (π / 180)

5. Calculate the chord length (L): L = 2 * R * sin(α_rad / 2)

Now, you have the chord length (L) for the given circular curve. When setting out the curve, you can measure the chord lengths and use them as an approximation of the curve. Keep in mind that this method assumes that the ground is level or that the elevations between the start and endpoints of the chords are adjusted accordingly.