Straight Line Between Two Points.xls

Purpose of calculation:
Find equation of a line given 2 coordinates

Calculation Reference
First principles

Calculation Validation
Independently checked.

Calculation Reference

Coordinate Geometry

Geometry of 2 Dimensions

To find the equation of a line given two coordinates, we can use the point-slope form of the equation of a line:

y - y1 = m(x - x1)

where (x1, y1) is one of the given coordinates, and m is the slope of the line.

To find the slope of the line, we can use the formula:

m = (y2 - y1) / (x2 - x1)

where (x2, y2) is the other given coordinate.

Once we have the slope, we can substitute it and one of the given coordinates into the point-slope form to get the equation of the line:

y - y1 = m(x - x1)

or we can rearrange it into the slope-intercept form:

y = mx + b

where b = y1 - mx1 is the y-intercept.

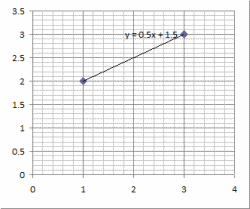
So, given two coordinates (x1, y1) and (x2, y2), the equation of the line passing through them is:

y - y1 = (y2 - y1) / (x2 - x1) * (x - x1)

or

y = (y2 - y1) / (x2 - x1) * (x - x1) + y1

or

y = mx + b

where m = (y2 - y1) / (x2 - x1) and b = y1 - m * x1.