Equilibrium of three forces in a plane.xls

Purpose of calculation:

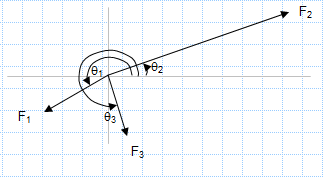
A force of known value F1 is in equilibrium with two other forces of unknown magnitude (F2 & F3).

All forces start at point o

The direction of F1 is from xo to x1.

The direction of F2 is from xo to x2.

The direction of F3 is from xo to x3.

Calculation Reference

First principles

Calculation Validation

All forces resolved vertically sum to zero - proof of vertical equilibrium.

All forces resolved horizontally sum to zero - proof of horizontal equilibrium.

Units

Calculations are in metric units.

Replace mm for in and N for lbf for imperial units.

Calculation Reference

Static Forces

When three forces act on an object in a plane, the object will be in equilibrium if the vector sum of the forces is zero. This means that the forces are balanced, and there is no net force acting on the object.

To determine the equilibrium of the forces, we can use vector addition. We add the three forces, vectorially, using the head-to-tail method. This means that we draw the vectors starting from a common point, and then add them by placing the tail of the second vector at the head of the first vector, and so on.

If the vector sum of the forces is zero, then the object is in equilibrium. This means that the forces cancel each other out, and there is no net force acting on the object.

If the vector sum of the forces is not zero, then the object is not in equilibrium. This means that there is a net force acting on the object, and it will accelerate in the direction of the net force.

To find the magnitude and direction of the net force, we can use the Pythagorean theorem and trigonometry. The magnitude of the net force is the length of the vector sum of the forces, and the direction is the angle that the vector sum makes with the horizontal axis.

It's important to note that the equilibrium of forces in a plane is a special case of the equilibrium of forces in three dimensions. In three dimensions, an object is in equilibrium if the vector sum of the forces and the vector sum of the torques are both zero.