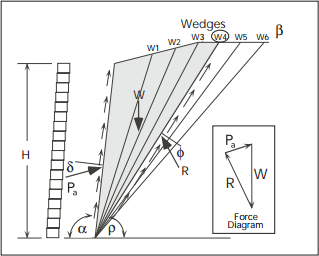
Coulomb Trial Wedge

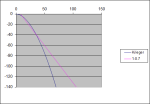
The limitation of closed form solutions, such as the Coulomb and Rankine equations, is that only simple level and in? nite sloping surcharges with uniform loadings can be analyzed. It is necessary to look at a “trial wedge” method or “approximation” method when attempting to analyze broken back slopes or other slope/load combinations. AASHTO and NCMA suggest an approximation method for broken-back slope conditions that de?nes equivalent design slopes for the external analysis. However, the internal analysis is not well de? ned for unusual slopes and loading conditions and the designer is expected to use engineering judgement with the simpli? ed methods. The KeyWall program uses a “trial wedge” analysis for determining the internal and external forces in order to provide the “correct” results for more complicated design geometries. The “trial wedge” calculation is an iterative process that determines the loading at successive failure plane orientations until a maximum loading is determined for the geometry and surcharge loading. The KeyWall “trial wedge” analysis used is consistent with the fundamental assumptions of the applicable Coulomb and Rankine theories by setting ? = ?. “Trial wedge” results match the equation solutions for the level and in?nite slope conditions, but will determine the “correct” internal and external values for broken back slope conditions and offset live and dead loads. This method of analysis permits the designer to properly model many typical design conditions and not overly simplify the analysis due to limitations of equation solutions and other design software.

Calculation Reference

Coulomb Trial Wedge

Retaining Wall Design

Lateral Earth Pressure Theories

Coulomb's Trial Wedge method is a popular method for calculating the stability of slopes, which is used in geotechnical engineering. The method is named after Charles-Augustin de Coulomb, who introduced it in the 18th century.

The Coulomb Trial Wedge method involves the following steps:

1. Divide the slope into a number of trial wedges, each with a different angle of inclination.
2. Calculate the driving force of each trial wedge by multiplying the weight of the soil in the wedge by the sine of the angle of inclination.
3. Calculate the resisting force of each trial wedge by multiplying the normal force on the slip surface by the coefficient of friction.
4. Calculate the factor of safety for each trial wedge by dividing the resisting force by the driving force.
5. Choose the trial wedge with the highest factor of safety as the critical wedge.
6. Calculate the critical angle of the slope by averaging the angles of the critical wedge and the adjacent wedges.

The Coulomb Trial Wedge method provides a simple and practical approach to analyzing slope stability, but it has several limitations. For example, it assumes that the soil is homogenous and that the failure plane is a straight line. In addition, it does not take into account the effect of pore water pressure or other factors that may affect the stability of the slope.

Overall, the Coulomb Trial Wedge method is a useful tool for preliminary analysis of slope stability, but it should be used in conjunction with other methods and engineering judgment to ensure the safety and stability of slopes in geotechnical engineering.